Die Windfahne wird so um ihre Vertikalachse gedreht und festgesetzt, dass sie im scheinbaren Wind senkrecht steht. Bei einer Kursabweichung schlägt sie infolge Seitenwind um ihre Achse aus, dreht über eine Vertikalschubstange und zwei Hebel einen in Pendelachse gelagerten Drehschaft, der wiederum das Servoruder um seine Hochachse dreht. Dadurch schwingt das Servoruder um die Pendelachse seitlich aus, bis es im stationären Zustand den Drehschaftwinkel erreicht.
Im Folgenden werden die geometrischen Zusammenhänge zwischen Kursabweichung, Windfahnen-Achsenneigung, Windfahnenrotation, Drehschaftrotation, Servoruderanstellung, Drehmomentoutput, Ruderkorrekturwinkel und Steuerweg wiedergegeben. Es werden die beiden gängigen Übertragungsprinzipien Z-Schaft-Mechanik sowie Kegelradübertragung mit der bei der WindGear-Anlage eingesetzten Murray-Gleitblockgelenkübertragung hinsichtlich der Kraftentwicklung bei unterschiedlichen Sollkursabweichungen verglichen.


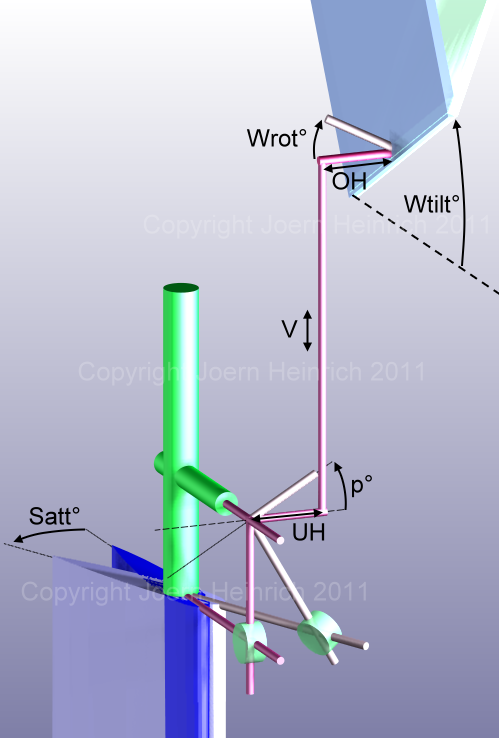
Kursfehler erzeugt Windfahnenrotation

Der Rotationswinkel der Windfahne (W_rot°) bei gegebener Abweichung vom Sollkurs (C_err°) ist nach Jan Alkema abhängig von der Krängung (H°), dem Kurs zum scheinbaren Wind (KZW°) und der Neigung der Windfahnenachse gegen die Horizontale (W_tilt°):

W_rot° = ARCTAN( TAN(C_err°) / SIN(W_tilt° + H° * SIN(KZW°)) )______________ [1]

KZW° ist im Bereich von 0°...180°, wobei 180° genau achterlichen scheinbaren Wind bedeutet und 90° einen annähernden Halbwindkurs.
W_tilt°, die Neigung der Windfahne gegen die Horizontale ist bei den meisten heutigen Windfahnensteuerungen ein Festwert und beträgt 20°.
C_err°, die Abweichung vom Sollkurs setzt die Windfahne einer Seitenwindkomponente aus und verursacht deren Rotation um ihre Achse.
W_rot°, die Windfahnenrotation, ist der Betrag, um den sich die Windfahne bei gegebener Kursabweichung dreht, um wieder parallel zu den Stromlinien im Wind zu stehen. Die maximale Windfahnenrotation ist wegen ihrer Hebelübertragung auf eine Vertikalschubstange begrenzt, Totpunkte gibt es bei +/-90°, denn weitere Drehung kann ein einfacher Hebel an einer Achse nicht in eine lineare Bewegung übertragen. Die meisten Windfahnen haben zur Vermeidung des Erreichens des oberen oder unteren Totpunktes sowie wegen der Gelenkenden der Übertragungshebel eine Limitierung der Windfahnenrotation bei ca. +/-50 bis +/-60°.


Windfahnenrotation erzeugt Drehschaftrotation

Wie weit eine Vertikalschubstange vom Hebel an der Windfahne auf- oder abbewegt wird (V), hängt sowohl von der Länge des Hebels (OH) als auch der Windfahnneigung gegen die Horizontale (W_tilt°) ab. Die Übertragung der Windfahnenrotation (W_rot°) über einen Hebel der Länge OH auf eine Vertikalschubstange lässt sich wie folgt beschreiben:

V = OH * COS(W_tilt°) * SIN(W_rot°)____________________________________[2]

Die Vertikalschubstange dreht durch ihre Auf-oder Abwärtsbewegung (V) über einen weiteren horizontalen Hebel der Länge UH den in der Pendelachse befindlichen Drehschaft um einen Winkel p°. Dieser Drehwinkel entspricht im stationären Zustand dem Pendelwinkel des Servoruders. Die Drehschaftdrehung in Abhängigkeit von der linearen Bewegung der Vertikalschubstange lässt sich beschreiben durch:

p° = ARCSIN( V / UH )______________________________________________[3]

mit Gleichung [2] zu:

p° = ARCSIN( OH / UH * COS(W_tilt°) * SIN(W_rot°) )_______________________[4]

Die Limitierungen der Windfahnenrotation definieren demnach gemeinsam mit der Neigung der Windfahnenachse gegen die horizontale, sowie dem Verhältnis der Hebel an Windfahne und Drehschaft den maximalen Pendelwinkel. Aus diesem ergibt sich mit der Servoausgangshebellänge damit der maximal von der Anlage erzeugten Steuerweg.


Drehschaftrotation erzeugt Servoruder-Anstellung

Den meisten heutigen Servo-Windfahnensteuerungen mit Horizontalwindfahne ist gemeinsam, dass an der Windfahne waagerecht ein Hebel befestigt ist, der über eine vertikale Schubstange einen Hebel an einem horizontalen, in der Pendelachse liegenden Drehschaft betätigt. Und diesen Drehschaft damit um einen bestimmten Winkelbetrag dreht. Die Übertragung dieses Drehschaftwinkels auf die Anstellung des Servoruders gegen die Schiffslängsachse ist jedoch unterschiedlich, gebräuchlich sind:

- Kegelradgetriebe (Bevel Gear)
- Z-Schaft Übertragung
- Murray-Gleitblockgelenk (WindGear)

Im Folgenden werden diese Transmissionsprinzipien hinsichtlich ihres relativen Servodrehmomentoutputs bei jeweils unterschiedlichen Sollkursabweichungen verglichen.


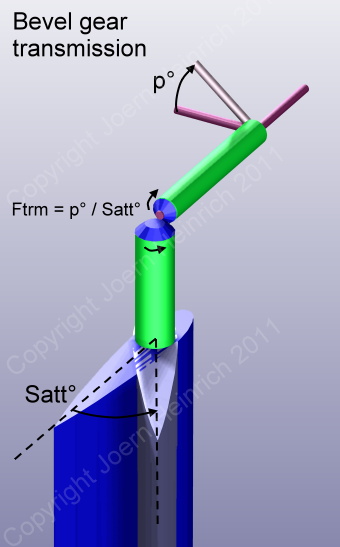
Kegelradgetriebe (Bevel Gear)

Beim Kegelradgetriebe sitzt am achteren Ende des horizontalen Drehschaftes ein Kegelrad, am oberen Ende des drehbaren Servoruderschaftes ein anderes. Dreht sich der Drehschaft, so wird dieser Drehwinkel (p°) auf die Servoruderanstellung (S_att°) im Untersetzungsverhältnis (F_trm) der beiden Kegelräder übertragen. Von den meisten Herstellern wird hierzu eine Untersetzung 1:0.5 (=2) eingesetzt, was bei einer Drehschaftdrehung um 10° einer Servoruderanstellung um 5° entspricht. Es ergibt sich der folgende einfache Zusammenhang zwischen Drehschaftrotation (p°) und Servoruderanstellung (S_att°):

S_att° = p° / F_{trm_____________________________________________________[5]}

Von Vorteil ist bei der Kegelradübertragung, dass man das Servoruder in Pendelrichtung unbegrenzt am Getriebe drehen kann, und damit seitlich aus dem Wasser herausschwenken kann. Nachteilig ist, dass sich das Spiel der Übertragungsmechanik schnell vergrößert, wenn die Achsenlagerungen - speziell das Servoruderlager Spiel bekommt. Die "Hebel" am Getriebe betragen üblicherweise um 15 bis 20 mm beim großen und 7 - 14 mm am kleinen Kegelrad. Ein kleines mechanisches Spiel bei derart kleinem Hebel wirkt sich störender auf die gesamte Hysterese der Anlage aus, als das gleiche Spiel bei einem größeren Hebel.


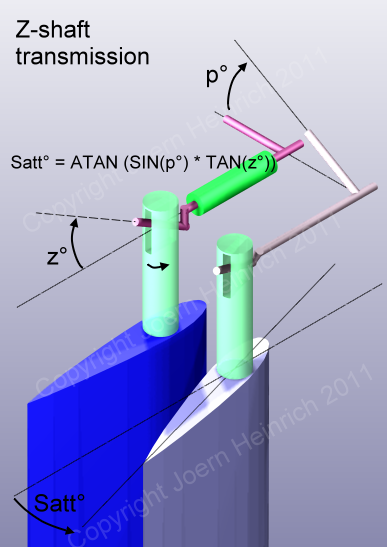
Z-Schaft Übertragung

Bei der Z-Schaft-Übertragung ist der Drehschaft Z-förmig gestaltet (liegendes Z). Der schräge Teil des Drehschaftes sitzt in einem vertikalen Schlitz im Servoruderschaft. Dreht sich der Drehschaft und kippt damit den schrägen Teil aus der vertikalen, so erfolgt ein Druck der Z-Schenkel an den gegenüberliegenden Innenseiten des Schlitzes und dreht den Servoruderschaft.
Der Drehwinkel bei der Z-Schaft-Übertragung ist wie folgt abhängig vom Winkel des schrägen Abschnitts des Drehschaftes (Z°) und der Drehschaftrotation (p°):

S_att° = ARCTAN (SIN(p°) * TAN(Z°))________________________________[6]

Bei der skizzierten, einfachen Z-Schaft Transmission wird die Kraft über eine sehr kleine Fläche im Schaftschlitz übertragen. Sofern dort nicht noch eine Gleitmuffe vorhanden ist, liegt der Z-Schaft nur mit seiner Rundung auf den Schlitzflanken auf. Er überträgt den größten Teil der Kraft nur außen am Schaftschlitz auf den Servoruderschaft. Gleichzeitig ist die Hebellänge hier nur im Bereich des Radius des Servoruderschaftes - also 15-25 mm, radial zum Drehschaft nur ein Drittel davon(!). Ein Wellenschlag auf das Servoruder, der jenes um die Hochachse gegen den Widerstand der Windfahne drehen will, trifft bei der Z-Schaft-Mechanik die winzigen Kontaktflächen zwischen Schlitz-Innenwänden und Z-Schaft mit hebelbedingt sehr hohem punktuellen Druck. Auch hier führt bereits geringes mechanisches Spiel zu einem großen toten Winkel (Hysterese) um die Steuer-Nullage.


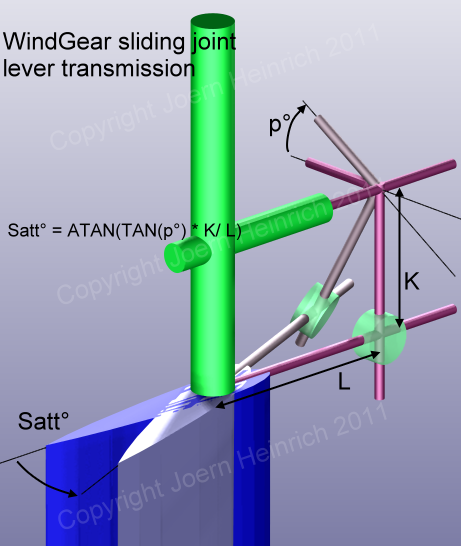
Murray-Gleitblockgelenk, rechtwinkliges Gestänge

Die Übertragung wird ausgeführt über ein zweiteiliges Gleitblockgelenk mit gegeneinander drehbaren Blöcken, die je eine Bohrung für einen Hebel haben. Das Gleitblockgelenk ist leicht verschiebbar auf den Hebeln. Am Drehschaft ist eine vertikale Steuerstange befestigt, die über das Gleitblockgelenk ihre Auslenkung auf die horizontale Servoruderpinne überträgt. Die Servoruderpinne dreht das Servoruder um seine Hochachse (S_att°).
Der Zusammenhang zwischen Drehschaftrotation(p°) und Servoruderanstellung (S_att°) lautet mit:
K = vertikaler Abstand des Gleitblockgelenkes von der Pendelachse
L = horizontaler Abstand des Gleitblockgelenkes von der Servoruder-Hochachse

S_att° = ARCTAN (TAN(p°) * K[mm] / L[mm] )_____________________________[7]



Bei dieser Übertragungsmechanik wirkt sich das Spiel im Übertragungselement in sehr geringem Maß auf die Hysterese (Gesamtspiel in der Übertragung) aus, weil die Hebel vergleichsweise lang sind.


Numerischer Vergleich der drei Übertragungsprinzipien

Die drei unterschiedlichen Übertragungsprinzipien erzeugen eine unterschiedliche Anstellung des Servoruders mit der Drehschaftrotation (p°). Die Steuerkraft des Servoruders jedoch ist proportional zu seinem Anstellwinkel (S_att°). Das heißt, dass die drei Übertragungsprinzipien einen unterschiedlichen Verlauf der Kraftentwicklung mit steigender Kursabweichung zeigen. Es werden für die Berechnungen eingesetzt:

- Windfahnen-Achsenneigung alle = 20°
- Z-Schaft-Mechanik hat 30° Z-Winkel
- Kegelradgetriebe hat Winkeluntersetzung 1:0,5
- Murray-Gestänge hat Geometrie K= 50 und L=100 [mm]

Die genannten Ausgangsbedingungen sind marktüblichen Anlagen entnommen und für die erzielten Anfangswinkel vergleichbar. Die Übertragung von Windfahnenrotation auf die Drehschaftrotation geht von identischen Rahmenbedingungen aus. Das Verhältnis von oberem Horizontalhebel zu unterem Horizontalhebel ist so gewählt (45 mm / 43 mm), dass die Windfahnenrotation in etwa der Drehschaftrotation entsprich.




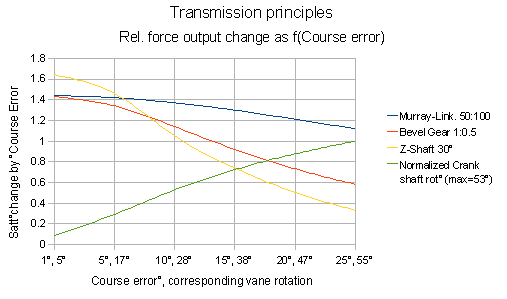
Auf der Y-Achse ist aufgetragen die Anstellwinkeländerung des Servoruders je °Kursfehler. Diese ist proportional zum Zuwachs an Kraftoutput je Grad zusätzlichem Kursfehler. Auf der X-Achse ist der absolute Kursfehler und die jeweils dazu korrespondierende steady-State Windfahnenrotation aufgetragen.
Klar ersichtlich ist, dass eine 30°-Z-Schaft-Mechanik bei geringen Kursfehlern kleiner als 7° bis 10° einen Vorteil gegenüber dem Murray-Link und dem Kegelradgetriebe bietet. Über 10° Kursfehler nimmt bei der Z-Schaft-Mechanik das je Grad Kursfehler zusätzlich erzeugte Servodrehmoment jedoch stärker ab.
Die Gestänge/Gleitblockübertragung (Murray-Link) startet bei gleicher Anfangskraftentwicklung wie das Kegelradgetriebe, doch weist bei stärkeren Kursabweichungen als 5° ein stärker steigendes Servodrehmoment als das Kegelradgetriebe auf. Bei einem Kursfehler von 15° erzeugt der Murray-Link je Grad zusätzlichem Kursfehler eine deutlich größere Servoruderanstellung.
Damit bietet der Murray-Link gegenüber den beiden anderen Prinzipien einen höheren nutzbaren Dynamikbereich des Windfahnenausschlags, der auch bei großen, schnellen weil wellenbedingten Sollkursabweichungen mit vergleichsweise stärkerem und schnellerem Gegenruder aufwartet.
Von der anderen Seite her betrachtet: Gerät eine Yacht mit einer Z-Schaft-Windselbststeuerung auf raumem Kurs durch eine schnelle Gierbewegung quer zur Welle, oder duch eine plötzliche Windänderung in einer Boe Amwind sehr rasch an das Ende des Windfahnenausschlags, so entwickelt das Servoruder dieser Anlage zum Gegensteuern weniger Kraft gegenüber der Anlage mit Murray-Gleitblockverbindung oder Kegelradgetriebe.
Andererseits ist bei einer Z-Schaft-Mechanik mit 30°-Z der Bereich der Kursabweichungen bis 5° schneller und damit präziser ausgesteuert als bei den beiden anderen Transmissionstypen. Vorausgesetzt war dabei ein 30°-Z-Schaft, eine 1:0.5-Kegelraduntersetzung und eine 50:100 Hebel-Geometrie.
Bei einem Kursfehler größer 12° unterschreitet die Z-Schaft-Mechanik die absolute Steuerkraft der Gleitblockübertragung, bei einem Kursfehler von schließlich 17° jene des Kegelradgetriebes (Auftragung der erzielten Servoruderanstellwinkel Satt° gegen den Kursfehler Cerr°):



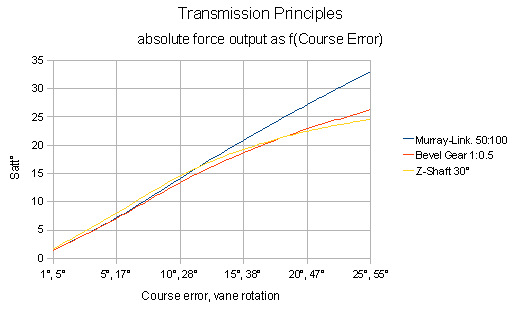
Es ist aus diesen erzielten Absolut-Anstellwinkeln des Servoruders ersichtlich, dass speziell für wendige Kurzkieler das Prinzip der Gleitblock-Hebelgestängeübertragung Vorteile bietet. Fälle, in denen ein Kursfehler schnell größer als 15° Grad wird, sind auf einer kleinen Fahrtenyacht im Seerevier wellenbedingt ab Bft 5-6 bereits häufig, besonders auf halbem bis achterlichem Kurs.



Variation der Hebelgestänge-Geometrie und Windfahnenneigung

Bei der WindGear-Anlage ist das Verhältnis von Steuerstangenlänge (L) zu Servopinnenlänge (K) nicht 50:100 sondern rechneroptimiert größer gewählt. Bei gleicher Neigung der Windfahnenachse von 20° ergibt sich das folgende Bild der WindGear-Geometrie im Vergleich zum 30°-Z-Schaft sowie zur 1:0.5 Winkeluntersetzung per Kegelradgetriebe:



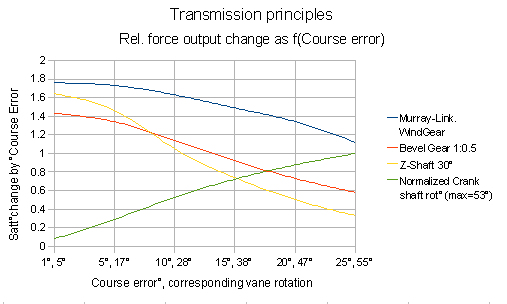
In der eingesetzten Windfahneneinstellung (alle mit 20° Neigung) ist bereits in der Nullage bei geringsten Kursabweichungen der Servodrehmoment-Zuwachs je Grad Kursabweichung der WindGear-Geometrie höher als sogar derjenige der Z-Schaft-Mechanik mit 30°-Z. Solche Einstellung der Windfahne bei 20° oder flacher, bietet sich bei der WindGear-Anlage zum Segeln bei schwachwindigen Bedingungen und geringer Schiffsgeschwindigkeit an.
Um zu vergleichbar kleinen Nullagen-Outputs zu kommen wie eine 30°-Z-Schaft- oder Kegelradmechanik mit Untersetzung = 2, wird bei der WindGear-Anlage die Neigung der Windfahnenachse per Stellschraube vergrößert, beispielsweise von obigen 20° auf 23°:



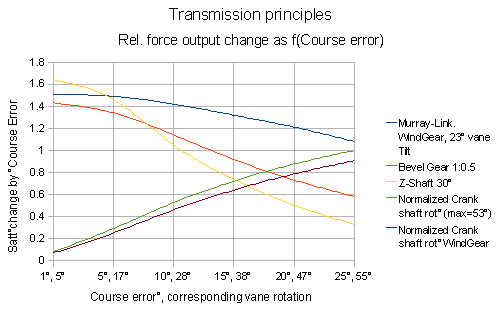
Und mit diesem kleinen Dreh an der Neigeeinrichtung für die Windfahnenachse hat man eine Einstellung des Kraftoutputs, die um die Nullage dem 30°-Z-Schaft sowie der 1:0.5-Kegelraduntersetzung ebenbürtig, jedoch zu größeren Kursabweichungen deutlich überlegen ist. Wegen der um 3° vergrößerten Neigung der Windfahnenachse verringert sich für den größten Kursfehler (25°) die Windfahnenrotation auf 52° (statt 55) , so dass durch diese bezüglich der Steuerkraft hocheffektive Einstellungsmaßnahme nur marginal etwas vom maximalen Steuerweg (=max Pendelwinkel 48° statt 53°) verlorengeht.

Joern Heinrich 04_2011